In diesem Abschnitt wird gezeigt, wie man einen Roboter mit dem allgemeinen Prinzip der proportionalen Fehlerkorrektur einer Linie mit unterschiedlich stark gekrümmten Kurven noch besser folgen lassen kann. Dabei werden wiederum die Grauwerte, also die Intensitäten von reflektiertem Licht eines Sensors des Quad RGB Sensors verwendet, um zu ermitteln, wie weit der Sensor von der Grenze zwischen schwarz und weiß entfernt ist.
Prinzip der proportionalen Fehlerkorrektur
Bei einem Regelkreis werden Messwerte oder Sensorinfotmationen so verarbeitet, dass diese bei der Steuerung von Aktionen, z. B. der Drehgeschwindigkeit von Motoren direkt einfließen. Damit ein Regelkreis seine Aufgabe erfüllt (z. B. das Erreichen und Halten einer bestimmten Temperatur bei eine Heizungssteuerung oder das exakte Fahren eines Roboters entlang einer Linie), muss es laufend Korrekturen geben.
Ausgegangen wird von einem gewünschten Sollwert, der beibehalten werden soll. Gibt es nun eine Abweichung von diesem Wert, so muss es eine Aktion geben, sodass sich die nächsten aktuellen Werte diesem Sollwert nähern. Damit solche Korrenturen nun nicht zu langsam ablaufen und der Sollwert nicht erreiht wird, oder mit einer Korrektur "über das Ziel hinausgeschossen" wird, kann bei Regelkreisen so vorgegangen werden, dass die Größe der Korrektur abhängig von der Größe des aktuellen Fehlers ist.
Das bedeutet: Je größer der Fehler zwischen einem aktuellen Wert und dem gewünschten Sollwert ist, desto stärker muss die Korrektur in Richtung des Sollwerts ausfallen.
Fehlerberechnung beim Folgen einer Linie mit einem Sensor
Befindet sich ein einzelner Sensor des Quad RGB Sensors genau über der Grenze zwischen weiß und schwarz, so liefert dieser einen Wert von 50. Ist der Sensor mehr über dem schwarzen Bereich, werden die Werte kleiner (die Intensität des reflektierten Lichts nimmt ab), ist der Sensor über dem weißen Bereich, werden die Werte größer (die Intensität des reflektierten Lichts nimmt zu).
Die Differenz zwischen dem gewünschten Sollwert 50 und dem aktuelle gemessenen Wert wird als Fehler bezeichnet.
Fehler = Sollwert - aktueller Wert
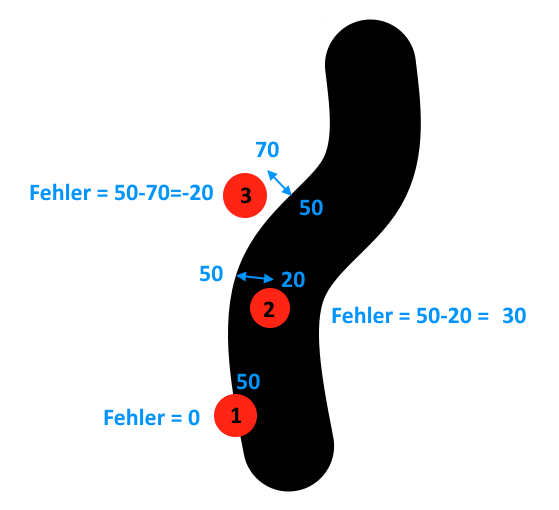
Position 1
Der Sensor befindet sich genau über der Grenze zwischen weiß und schwarz. Der aktuelle Wert 50 entspricht dem Sollwert 50. Die Differenz ist 0 und somit ist der Fehler = 0.
Fehler = Sollwert - aktueller Wert = 50 - 50 = 0
Hier ist keine Korrektur notwendig, der Roboter soll geradeaus fahren, die beiden Motoren sollen sich also gleich schnell drehen.
Position 2
Der Sensor befindet sich rechts von der Grenze zwischen weiß und schwarz und der aktuelle Wert des Sensors beträgt 20. Die Differenz zwischen Sollwert und aktuellem Wert beträgt hier 30.
Fehler = Sollwert - aktueller Wert = 50 - 20 = 30
Damit sich der Sensor in Richtung des Sollwerts bewegt, muss sich der Roboter nach links bewegen. Der linke Motor muss sich langsamer drehen, der rechte Motor muss sich schneller drehen.
Position 3
Hier befindet sich der Sensor links der Grenze zwischen weiß und schwarz, der aktuelle Wert des Sensors beträgt hier 70 und der Fehler somit -20.
Fehler = Sollwert - aktueller Wert = 50 - 70 = -20
In diesem Fall muss sich der Roboter nach rechts drehen, damit der Sensor zum Sollwert direkt auf der Grenze bewegt wird. Der linke Motor muss sich schneller drehen und der rechte Motor muss sich langsamer drehen.
Proportionale Korrektur der Motorgeschwindigkeiten
Aus den beiden Fällen Position 2 und Position 3 in der Abbildung ergibt sich, dass jeweils die Umdrehungsgeschwindigkeit eines Motors vergrößert und des anderen entgegengesetzt verkleinert werden muss, damit sich der Sensor in Richtung des Sollwerts bewegt und somit der Fehler wieder kleiner wird. Ist der Fehler größer, muss es eine stärkere Korrektur der Motorgeschwindigkeiten geben, ist der Fehler kleiner, so muss die Korrektur der Motorgeschwindigkeiten nicht so groß ausfallen, damit sich der Roboter nicht zu weit dreht.
Die aktuelle Größe des Fehlers kann direkt für die Korrektur der Motorgeschwindigkeiten anhand einer einfachen Berechnung herangezogen werden. Ausgehend von einer festgelegten Startgeschwindigkeit der beiden Motoren wird jeweils ein Betrag des Fehlers, multipliziert mit einem Proportionalitätsfaktor P dazugezählt oder abgezogen.
M1 speed aktuell = M1 speed start + Fehler * P
M2 speed aktuell = M2 speed start - Fehler * P
Im Rahmen einer konkreten praktischen Aufgabenstellung besteht die Herausforderung nun darin, einem optimalen Wert für den Proportionalitätsfaktor P zu finden.
Dieser Proportionalitätsfaktor P kann größer 1 sein, wenn der Wert eines Fehlers zu klein ist, damit dieser Korrekturwerte ergibt, die groß genug sind oder er kann aber auch kleiner 1 sein, wenn der Wert des aktuellen Fehlers vermindert werden muss, da die sich daraus ergebende Korrekturwerte zu groß sind.
- P < 1: Korrekturwerte sind proportional dem Fehler und kleiner als der Fehler
- P = 1: Korrekturwerte entsprechen genau dem Fehler
- P > 1: Korrekturwerte sind proportional dem Fehler und größer als der Fehler
In der folgenden Tabelle wird gezeigt, welchen Einfluss unterschiedliche Proportionalitätsfaktoren P (P = 1, P = 0.5 und P = 2) auf die damit berechneten Korrekturwerte in Bezug auf den vorliegenden Fehler haben.
| Fehler | Motorgeschwindigkeiten (P = 1) | Fehler | Motorgeschwindigkeiten (P = 0.5) |
Fehler | Motorgeschwindigkeiten (P = 2) | ||
| 0 | M1 = 50 + 0 * 1 = 50 M2 = 50 - 0 * 1 = 50 |
0 | M1 = 50 + 0 * 0.5 = 50 M2 = 50 - 0 * 0.5 = 50 |
0 | M1 = 50 + 0 * 2 = 50 M2 = 50 - 0 * 2 = 50 |
||
| 1 | M1 = 50 + 1 * 1 = 51 M2 = 50 - 1 * 1 = 49 |
1 | M1 = 50 + 1 * 0.5 = 50.5 M2 = 50 - 1 * 0.5 = 49.5 |
1 | M1 = 50 + 1 * 2 = 52 M2 = 50 - 1 * 2 = 48 |
||
| 2 | M1 = 50 + 2 * 1 = 52 M2 = 50 - 2 * 1 = 48 |
2 | M1 = 50 + 2 * 0.5 = 51 M2 = 50 - 2 * 0.5 = 49 |
2 | M1 = 50 + 2 * 2 = 54 M2 = 50 - 2 * 2 = 46 |
||
| 3 | M1 = 50 + 3 * 1 = 53 M2 = 50 - 3 * 1 = 47 |
3 | M1 = 50 + 3 * 0.5 = 51.5 M2 = 50 - 3 * 0.5 = 48.5 |
3 | M1 = 50 + 3 * 2 = 56 M2 = 50 - 3 * 2 = 44 |
||
| 4 | M1 = 50 + 4 * 1 = 54 M2 = 50 - 4 * 1 = 46 |
4 | M1 = 50 + 4 * 0.5 = 52 M2 = 50 - 4 * 0.5 = 48 |
4 | M1 = 50 + 4 * 2 = 58 M2 = 50 - 4 * 2 = 42 |
||
| 5 | M1 = 50 + 5 * 1 = 55 M2 = 50 - 5 * 1 = 45 |
5 | M1 = 50 + 5 * 0.5 = 52.5 M2 = 50 - 5 * 0.5 = 47.5 |
5 | M1 = 50 + 5 * 2 = 60 M2 = 50 - 5 * 2 = 40 |
||
| 10 | M1 = 50 + 10 * 1 = 60 M2 = 50 - 10 * 1 = 40 |
10 | M1 = 50 + 10 * 0.5 = 55 M2 = 50 - 10 * 0.5 = 45 |
10 | M1 = 50 + 10 * 2 = 70 M2 = 50 - 10 * 2 = 30 |
||
| 20 | M1 = 50 + 20 * 1 = 70 M2 = 50 - 20 * 1 = 30 |
20 | M1 = 50 + 20 * 0.5 = 60 M2 = 50 - 20 * 0.5 = 40 |
20 | M1 = 50 + 20 * 2 = 90 M2 = 50 - 20 * 2 = 10 |
Der Proportionalitätsfakor P muss so gewählt werden, dass die Regelung in einem System - z. B. Motorgeschwindigkeit + / - Korrekturwert - so verläuft, dass ein Sensor in Abhängigkeit unterschiedlich großer Fehler so schnell wie möglich wieder Werte des Sollwerts liefert.
Dies kann beim Fahren eines Roboter entlang einer Linie experimentell ermittelt werden und muss selbstverständlich an die unterschiedlichen Krümmungen der Linie eines vorliegenden Kurververlaufs speziell angepasst werden.
Beispiel - Folgen einer Linie mit einem Sensor und proportionaler Fehlerkorrektur
Mit dem folgenden Code-Beispiel liegt ein vollständiges und funktionierende Skript vor, das mit einem mBot2 Roboter auf der Originalbahn, die dem Roboter begelegt ist, getestet werden kann. Dabei handelt es sich um die zuvor beschriebene Umsetzung des Verfahrens der proportionalen Fehlerkorrektur.
Zu Beginn werden alle relevanten Werte in Variablen abgelegt. Es sind dies die Grundgeschwindigkeiten der Motoren mit denen diese grundsätzlich geradeaus fahren, der Sollwert für die gewünschte und optimale Position des Sensor in Bezug auf die schwarze Linie und der Proportionaltätsfaktor.
Zum bestmöglichen Folgen einer vorgegebenen Linie ist der optimale Proprtionalitätsfaktor experimentell zu ermitteln. Dieser muss auch neu bestimmt werden, wenn der Roboter mit einer anderen Grundgeschwindigkeit fahren soll.
In der while-Schleife befindet sich der eigentliche Regelkreis mit dem Einlesen des aktuellen Sensorwerts, über die Berechung des Fehlers und der Motorgeschwindigkeiten unter Berücksichtigung einer proportionalen Fehlerkorrektur bis zum Setzen der Motorgeschwindigkeiten.
import cyberpi, mbot2, mbuildfloat_m1_start = 20float_m2_start = 20int_sollwert = 50float_p = 0.5while True:int_s2 = mbuild.quad_rgb_sensor.get_gray(2)int_fehler = int_sollwert - int_s2float_m1 = float_m1_start + int_fehler * float_pfloat_m2 = float_m2_start - int_fehler * float_pmbot2.EM_set_speed(float_m1,1)mbot2.EM_set_speed(-float_m2,2)
Erklärungen zu diesem Skript
1: import cyberpi, mbot2, mbuild
Import der Module cyberpi, mbot2 (Motoren) und mbuild (Quad RGB Sensor)
3: float_m1_start = 20
4: float_m2_start = 20
Hier wird in den beiden Varialben die Grundgeschwindigkeit der beiden Motoren abgelegt. Diese soll 20 RPM betragen.
6: int_sollwert = 50
In der Variable int_sollwert wird der Grauwert abgelegt, der von einem Sensor genau am Übergang zwischen weiß und schwarz ermittelt wird.
8: float_p = 0.5
In der Variable float_p wird der Proportionalitätsfaktor abgelegt, mit dem der aktuelle Fehler multipliziert wird um den Korrekturwert für die Motorgeschwindigkeiten zu erhalten.
12: int_s2 = mbuild.quad_rgb_sensor.get_gray(2)
In dieser Zeile wird der aktuelle Grauwert, den der Sensor 2 ermittelt, in der Variable int_s2 abgelegt.
14: int_fehler = int_sollwert - int_s2
Nachdem der aktuelle Grauwert bekannt ist, wird mit der Differenz zwischen dem Sollwert und dem aktuellen Grauwert der aktuelle Fehler berechnet.
16: float_m1 = float_m1_start + int_fehler * float_p
17: float_m2 = float_m2_start - int_fehler * float_p
Mit dem aktuellen Fehler und dem zuvor festgelegten Proportionalitätsfaktor wird der Korrekturwert berechnet und zur festgelegten Grundgeschwindigkeit dazugezählt bzw. bei der des anderen Motors abgezogen. Diese aktuell berechneten Motorgeschwindigkeiten werden in den Varialben float_m1 und float_2 abgelegt.
19: mbot2.EM_set_speed(float_m1,1)
20: mbot2.EM_set_speed(-float_m2,2)
Nun werden die neu berechneten Motorgeschwindigkeiten mit der Funktion mbot2.EM_set_speed(speed, port) für den Motor 1 (=linker Motor) und den Motor 2 (=rechter Motor) gesetzt. Dabei ist zu beachten, dass die Geschwindigkeit für den rechten Motor mit -1 multipliziert - also vor den Wert ein - gesetzt werden muss - wird, damit sich dieser in die richtige Richtung dreht.
